La beetheory : Une nouvelle façon de comprendre la gravité

Et si la gravité n’était pas une force, mais un effet de l’interférence des ondes ?

La théorie de l’abeille est un cadre innovant qui modélise la gravité à l’aide de principes quantiques basés sur les ondes.
Elle ne s’appuie pas sur des particules comme le graviton, mais explique l’attraction gravitationnelle comme le résultat de l’interférence entre les fonctions d’onde. Cette approche remet en question les paradigmes classiques et relativistes, offrant une nouvelle voie vers l’unification des forces fondamentales de la nature.

Pourquoi réimaginer la gravité ?

La gravité a longtemps été décrite, mais jamais vraiment expliquée.

  • Newton l’a modélisée comme une force d’attraction entre des masses.
  • Einstein l’a reformulé en parlant de la courbure de l’espace-temps causée par la masse.

Ces théories sont puissantes, mais elles laissent des questions essentielles sans réponse :

  • Pourquoi la gravité existe-t-elle ?
  • Pourquoi ne pouvons-nous pas l’annuler ou la bloquer ?
  • Pourquoi est-elle si faible par rapport aux autres forces ?
  • Pourquoi ne pouvons-nous pas la réconcilier avec la mécanique quantique ?

BeeTheory offre une nouvelle perspective.

Jets de plasma des trous noirs - La théorie des abeilles explore l'influence de la dynamique des ondes quantiques sur les jets de haute énergie éjectés par les trous noirs.

L’idée maîtresse de BeeTheory

Chaque particule peut être décrite par une fonction d’onde.
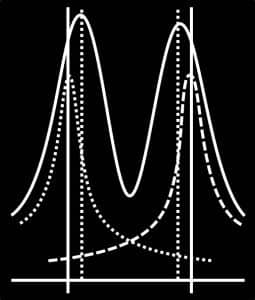
Lorsque deux particules sont proches l’une de l’autre, leurs fonctions d’onde se chevauchent légèrement.
Cette interférence crée un mouvement directionnel net, attirant chaque particule vers l’autre – un phénomène que nous connaissons sous le nom de gravité.

La gravité, dans la théorie de l’abeille, n’est pas médiée par des particules.
Elle émerge naturellement des interactions ondulatoires.

Cela conduit à :

  • Un modèle de gravité sans gravitons
  • Une explication basée sur les ondes compatible avec la théorie quantique
  • Un cadre pour la modélisation de la gravité à toutes les échelles
Théorie de l'abeille - Un modèle basé sur les ondes qui explore la gravité, la mécanique quantique et la nature interconnectée de l'univers.

Un modèle gravitationnel basé sur les ondes et fondé sur la physique

La théorie de l’abeille est fondée sur :

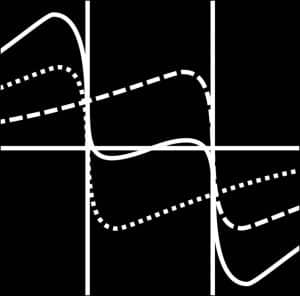
  • L’équation de Schrödinger en 3D, pour décrire les particules comme des fonctions d’onde dans l’espace
  • Produits de convolution, pour représenter l’interférence des ondes
  • Une structure mathématique qui remplace le concept de champ de force par une dynamique d’interaction d’ondes.

Il est ainsi possible de simuler :

  • L’émergence des champs gravitationnels
  • Mouvement des particules entraîné par la convergence des vagues
  • Propagation des ondes à l’échelle quantique et cosmologique

Ce que BeeTheory change

Passer des particules aux ondes

  • Pas de graviton nécessaire
  • La gravité est un effet émergent et non une force fondamentale

Une voie vers l’unification

  • L’électromagnétisme, la gravité et les champs quantiques pourraient tous découler d’un cadre ondulatoire unique

Des réponses à des mystères non résolus

  • Explique les phénomènes tels que la matière noire comme des effets de structures ondulatoires invisibles
  • Lumière sur les jets de plasma, les asymétries galactiques et les impulsions gravitationnelles d’origine ondulatoire
  • Permet de comprendre pourquoi la gravité se comporte comme elle le fait
Théorie de l'abeille - Un modèle basé sur les ondes qui redéfinit la gravité, la mécanique quantique et l'interconnexion universelle

Un univers tissé de vagues

Au-delà des équations, la théorie de l’abeille propose une vision différente de la réalité.
Au lieu de particules et de champs séparés, nous voyons un tissu continu d’interactions ondulatoires.

Cela implique :

  • Une connexion transparente à toutes les échelles – de l’échelle subatomique à l’échelle galactique
  • Une réinterprétation de la matière, de l’énergie et de la conscience en tant qu’expressions ondulatoires
  • Un changement philosophique vers l’unité et l’interconnexion

La vague ne porte pas la réalité.
La vague est la réalité.

Théorie de l'abeille - Exploration de la gravité basée sur les ondes, de la mécanique quantique et de l'interconnexion universelle par le biais de la résonance et de la dynamique de l'espace-temps
Stratégies d'observation pour valider la théorie de l'abeille - Explorer les méthodes scientifiques pour tester la gravité basée sur les ondes, l'interconnexion quantique et la dynamique de l'espace-temps.

Explorez la théorie des abeilles en profondeur

Fondements

Implications

Boutons CTA à inclure :
→ Lisez les articles complets
→ Voir les simulations en 3D
→ Téléchargez le résumé PDF

test