벌 이론: 중력을 이해하는 새로운 방법
중력이 힘이 아니라 파동 간섭의 영향이라면 어떨까요?
비이론은 파동 기반 양자 원리를 이용해 중력을 모델링하는 혁신적인 프레임워크입니다.
중력 이론은 중력자와 같은 입자에 의존하지 않고 파동 함수 간의 간섭으로 중력의 인력을 설명합니다. 이 접근 방식은 고전 및 상대론적 패러다임에 도전하여 자연의 근본적인 힘을 통합하는 새로운 길을 제시합니다.

왜 중력을 새롭게 상상해야 할까요?
중력은 오랫동안 설명되어 왔지만 제대로 설명된 적은 없습니다.
- 뉴턴은 이를 질량 사이의 인력으로 모델링했습니다.
- 아인슈타인은 이를 질량에 의한 시공간 곡률로 재구성했습니다.
이러한 이론은 강력하지만 본질적인 질문에 대한 답을 제시하지 못합니다:
- 중력은왜 존재할까요?
- 취소하거나 차단할 수 없는 이유는 무엇인가요?
- 다른 세력에 비해 왜 그렇게 약한가요?
- 양자역학과 조화시킬 수 없는 이유는 무엇일까요?
BeeTheory는 새로운 관점을 제시합니다.

BeeTheory의 핵심 인사이트
모든 입자는 파동 함수로 설명할 수 있습니다.
두 입자가 서로 가까이 있으면 파동 함수가 약간 겹칩니다.
이 간섭은 순방향 운동을 일으켜 각 입자를 서로 끌어당기는데, 이 현상을 중력이라고 합니다.
벌이론에서 중력은 입자에 의해 매개되지 않습니다.
중력은 파동의 상호작용에서 자연스럽게 나타납니다.
이는 다음과 같이 이어집니다:
- 중력이 필요 없는 중력 모델
- 양자 이론과 호환되는 파동 기반 설명
- 모든 규모의 중력 모델링을 위한 프레임워크
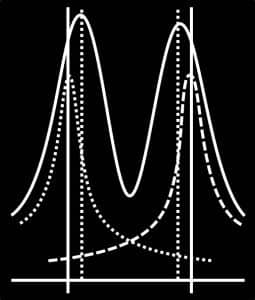

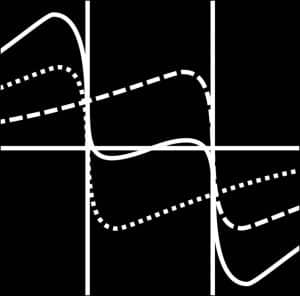
물리학에 기반한 파동 기반 중력 모델
BeeTheory를 기반으로 합니다:
- 입자를 공간의 파동 함수로 설명하는 3D 슈뢰딩거 방정식
- 컨볼루션 곱, 파동 간섭을 표현하기 위해
- 역장의 개념을 파동 상호작용 역학으로 대체하는 수학적 구조
이를 통해 시뮬레이션이 가능합니다:
- 중력장의 출현
- 파동 수렴으로 구동되는 파티클 모션
- 양자 및 우주론적 규모에서의 파동 전파
BeeTheory의 변화
입자에서 파동으로의 전환
- 그래비톤 필요 없음
- 중력은 근본적인 힘이 아닌 일시적인 효과입니다.
통일을 향한 길
- 전자기학, 중력, 양자장은 모두 단일 파동 기반 프레임워크에서 비롯될 수 있습니다.
풀리지 않는 미스터리에 대한 해답
- 암흑 물질과 같은 현상을 보이지 않는 파동 구조의 효과로 설명합니다.
- 플라즈마 제트, 은하 비대칭성, 파동 기반 중력 펄스에 대해 조명합니다.
- 중력이 왜 그런 식으로 작동하는지에 대한 인사이트를 제공합니다.
파도가 엮어낸 우주
비이론은 방정식을 넘어 현실에 대한 다른 관점을 제안합니다.
입자와 장이 분리된 것이 아니라 파동의 상호작용으로 이루어진 연속적인 구조를 봅니다.
이는 다음을 의미합니다:
- 아원자부터 은하계까지모든 규모에 걸쳐 원활한 연결
- 물질, 에너지, 의식을 파동 기반 표현으로 재해석한 작품
- 통합과 상호 연결성을 향한 철학적 전환
파도는 현실을 전달하지 않습니다.
물결이 현실입니다.


BeeTheory 자세히 살펴보기
기초
시사점
포함할 CTA 버튼
→ 전체 기사 읽기
→ 3D 시뮬레이션 보기
→ 요약 PDF 다운로드